For corporate bond investors one of the most important points of discussion is spreads. Spreads are the industry term for the risk premium an investor aims to earn in the corporate bond market. It is the difference between the yield a bond is promising and the risk-free rate. If spreads are narrowing it is positive for investors as the price of the corporate bond will increase; likewise, a widening leads to a lower bond price. Although the concept sounds simple, the devil is in the details, as investors have different definitions of a risk-free rate and different methods of calculating credit spreads.
For example, in the US market investors compare corporate bond yields to the yield of the closest “on-the-run” US Treasury bond. This approach is a common market practice but has several flaws. Firstly, the maturity of the corporate bond might be different to the Treasury bond and this difference in maturity will impact the calculated spread. The maturity mismatch makes it difficult to use the spread for relative value analysis, i.e. a credit spread comparison between two telecom companies. The difference between spreads might not only be due to a deviation in credit quality but also by the way the spread is calculated. The second flaw comes from the fact that corporate and government bonds might have different coupons. Even if both bonds have the same maturity or investors use an interpolated government bond curve1, we would still have a mismatch in duration and convexity.
1Interpolated Government Bond Curve: Interpolated refers to the methods used to create new estimated data points between known data points on a graph. “On the run” Treasury bond yields will be used to create an interpolated curve and estimate theoretical yield level for maturities in between to Treasury bonds.

Source: Shutterstock
In the European corporate bond market, a different benchmark is used to evaluate credit quality: the I-Spread (Interpolated Spread). To derive the I-Spread, investors calculate the difference between a bond yield and the corresponding point on an interpolated swap curve. But similar to the US market example discussed above, the I-Spread is not a flawless measure of credit quality. First of all, whether the swap curve can be used as an indicator of the risk-free rate is questionable as it also reflects the counter-party risk of dealing with the banking sector. In addition, it only measures the distance between a bond yield and the corresponding point on the interpolated swap curve. This simplification leads to the shape of the yield curve not being recognised in the calculation of the spread.
The criticism of these widely used spread measures beckons the question: are there better ways to assess credit quality? The ASW spread (asset swap spread) and the Z-spread/OAS-spread are, in our opinion, better ways of measuring credit quality. The ASW spread assumes a combination between a cash bond and an interest rate swap. The spread represents the difference between the present value of a bond cash flow, discounted using a swap zero curve2, and its market price. The ASW represents a good way to evaluate credit quality with one caveat, it only works when bonds are trading close to par. Applying it to bonds trading at a significant discount or premium would lead to an incorrect outcome. Therefore, most corporate bond investors now prefer the Z-spread (zero-volatility spread) which is not impacted by the bond’s price. The Z-spread is the basis point spread that needs to be added to either a swap zero or government bond zero curve, such that the sum of the corporate bond’s discounted cash flows equals its current market price. The Z-spread is not just using the YTM (yield to maturity) to discount, but also includes the term structure of the bond market. Sometimes investors also use a derivative of the Z-spread to measure the credit risk premium, the OAS-spread (option adjusted spread). The OAS-spread equals the Z-spread plus or minus the value of embedded bond options, i.e. make- whole call (MWC) (Chart 1). Option pricing models are used to derive the value of the embedded options.
2A swap zero curve assumes that all bonds on the curve have a zero coupon. The assumption is used to overcome the problem of duration and convexity miss match which was discussed earlier.
Chart 1: Z spread and OAS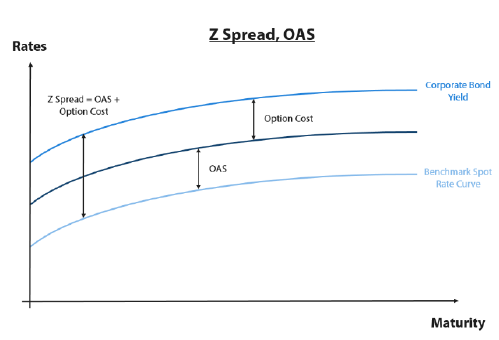
Source: Nikko AM
Regardless of the spread used to compare two bonds or to analyse price moves in the corporate bond market, it is important to be consistent with the spread being used and to be aware of potential flaws. It is also important to remember that some spread measures are more preferable than others. We favour the use of the ASW-spread or the Z-spread/OAS-spread to assess credit risk.




